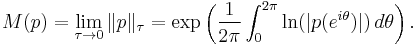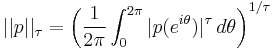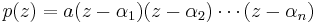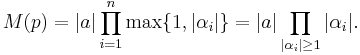Mahler measure

In mathematics, the Mahler measure M(p) of a polynomial p is

$M(p)=\lim_{\tau \rightarrow 0} \|p\|_{\tau} = \exp\left( \frac{1}{2\pi} \int_{0}^{2\pi} \ln(|p(e^{i\theta})|)\, d\theta \right).$

Here p is assumed complex-valued and

$||p||_{\tau} =\left( { \frac{1}{2\pi} \int_{0}^{2\pi} |p(e^{i\theta})|^\tau \, d\theta } \right)^{1/\tau} \,$

is the L_τ norm of p (although this is not a true norm for values of τ < 1).

It can be shown that if

$p(z) = a(z-\alpha_1)(z-\alpha_2)\cdots(z-\alpha_n)$

then

$M(p) = |a| \prod_{i=1}^{n}\max\{1,|\alpha_i|\}=|a|\prod_{|\alpha_i| \ge 1} |\alpha_i|.$

The Mahler measure of an algebraic number α is defined as the Mahler measure of the minimal polynomial of α over Q.

The measure is named after Kurt Mahler.

Properties

The Mahler measure is multiplicative, i.e. M(pq) = M(p)M(q).
(Kronecker's Theorem) If p is an irreducible monic integer polynomial with 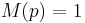$M(p) = 1$ , then either p(z)=z, or p is a cyclotomic polynomial.

Hazewinkel, Michiel, ed. (2001), "Mahler measure", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=m120070
Peter Borwein (2002). Computational Excursions in Analysis and Number Theory. CMS Books in Mathematics. Springer-Verlag. pp. 3, 15. ISBN 0-387-95444-9.
J.L. Jensen (1899). "Sur un nouvel et important théorème de la théorie des fonctions". Acta Mathematica 22: 359–364. doi:10.1007/BF02417878.
Knuth, Donald E (1997). "4.6.2 Factorization of Polynomials". Seminumerical Algorithms. The Art of Computer Programming. 2 (Third ed.). Reading, Massachusetts: Addison-Wesley. pp. 439–461, 678–691. ISBN 0-201-89684-2.
M.J. Mossinghoff (1998). "Polynomials with Small Mahler Measure". Mathematics of Computation 67 (224): 1697–1706. doi:10.1090/S0025-5718-98-01006-0.